在数学的众多分支中，密度函数规范性是一个重要的概念，它涉及到概率论、统计学以及相关的数学领域，本文将探讨密度函数规范性的定义、性质、应用，以及其在实际问题中的意义。

密度函数规范性的定义与性质

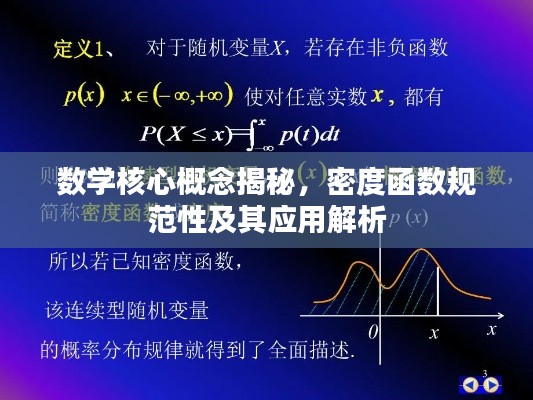
在概率论和统计学中，密度函数是对随机变量的概率分布进行描述的函数，密度函数规范性指的是该函数在满足一定条件下的标准化特性，即概率密度函数在整个实数轴上的积分等于1，这是概率密度函数的一个基本性质，保证了概率的完备性和规范性。

密度函数规范性的应用

密度函数规范性在概率论和统计学中有着广泛的应用，它是构建概率模型的基础，通过密度函数规范性，我们可以描述随机变量的分布特征，进而构建概率模型，解决实际问题，密度函数规范性在统计推断中发挥着重要作用，在参数估计和假设检验中，我们需要利用样本数据的概率分布信息，而密度函数规范性为我们提供了这一信息，密度函数规范性还在风险评估、决策分析等领域有着广泛的应用。

密度函数规范性与实际问题

密度函数规范性在实际问题中有着重要意义，它可以用于描述自然现象的不确定性，在气象、地震等自然灾害预测中，我们可以通过密度函数规范性描述事件的发生概率，进而进行风险评估，密度函数规范性在金融市场中的应用也非常广泛，我们可以利用密度函数规范性描述股票价格的波动概率，进行投资决策分析，密度函数规范性还在生物统计学、医学诊断等领域发挥着重要作用。

案例分析

假设我们有一个关于某地区降雨量的数据集，我们想要了解降雨量的分布情况，通过构建密度函数并验证其规范性，我们可以描述降雨量的概率分布特征，进而进行风险评估和预测，我们可以利用正态分布的概率密度函数来描述降雨量数据，通过检验其规范性，我们可以确定模型的适用性，并进一步研究降雨量的分布特征。

本文探讨了密度函数规范性的定义、性质、应用以及在实际问题中的意义，密度函数规范性作为概率论和统计学中的核心概念，为我们描述随机变量的概率分布提供了有力工具，通过密度函数规范性，我们可以构建概率模型，解决实际问题，并在风险评估、决策分析等领域发挥重要作用，随着数据科学和人工智能的不断发展，密度函数规范性的应用将更加广泛，为我们解决更多实际问题提供有力支持。